Iterating over multiple refutation tests
The objective of this notebook is to compare the ability of refuters to detect the problems in a given set of estimators. Note: This notebook makes use of the optional dependencies: - pygraphviz - econml
Import Dependencies
[23]:
from dowhy.datasets import linear_dataset
from dowhy import CausalModel
import econml
# Config dict to set the logging level
import logging.config
DEFAULT_LOGGING = {
'version': 1,
'disable_existing_loggers': False,
'loggers': {
'': {
'level': 'WARN',
},
}
}
logging.config.dictConfig(DEFAULT_LOGGING)
# Disabling warnings output
import warnings
from sklearn.exceptions import DataConversionWarning
warnings.filterwarnings(action='ignore', category=DataConversionWarning)
Inspection Parameters
These parameters give us the option of inspecting the intermediate steps to sanity check the steps performed
[24]:
inspect_datasets = True
inspect_models = True
inspect_identified_estimands = True
inspect_estimates = True
inspect_refutations = True
Estimator List
We pass a list of strings, corresponding to the estimators of interest
[25]:
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LassoCV
from sklearn.ensemble import GradientBoostingRegressor
estimator_list = ["backdoor.propensity_score_matching", "backdoor.propensity_score_weighting", "backdoor.econml.dml.DML"]
method_params= [ None, None, {"init_params":{'model_y':GradientBoostingRegressor(),
'model_t': GradientBoostingRegressor(),
"model_final":LassoCV(fit_intercept=False),
'featurizer':PolynomialFeatures(degree=1, include_bias=False)},
"fit_params":{}} ]
Refuter List
A list of strings, corresponding to each refuter we wish to run
[26]:
refuter_list = ["bootstrap_refuter", "data_subset_refuter"]
Create the Datasets
[27]:
# Parameters for creating the Dataset
TREATMENT_IS_BINARY = True
BETA = 10
NUM_SAMPLES = 5000
NUM_CONFOUNDERS = 5
NUM_INSTRUMENTS = 3
NUM_EFFECT_MODIFIERS = 2
# Creating a Linear Dataset with the given parameters
linear_data = linear_dataset(
beta = BETA,
num_common_causes = NUM_CONFOUNDERS,
num_instruments = NUM_INSTRUMENTS,
num_effect_modifiers = NUM_EFFECT_MODIFIERS,
num_samples = NUM_SAMPLES,
treatment_is_binary = True
)
# Other datasets come here
# Append them together in an array
datasets = [linear_data]
Inspect Data
[28]:
dataset_num = 1
if inspect_datasets is True:
for data in datasets:
print("####### Dataset {}###########################################################################################".format(dataset_num))
print(data['df'].head())
print("#############################################################################################################")
dataset_num += 1
####### Dataset 1###########################################################################################
X0 X1 Z0 Z1 Z2 W0 W1 W2 \
0 1.967335 1.905424 1.0 0.670757 0.0 -0.202865 -1.144348 1.183711
1 1.128093 -1.239441 0.0 0.867080 0.0 -0.356516 1.708609 1.092528
2 1.652412 -0.091724 1.0 0.571701 0.0 -0.932946 -2.417561 0.628134
3 -1.435738 0.029290 1.0 0.107491 0.0 -0.573645 -1.436408 -0.625384
4 1.811213 0.656676 1.0 0.789946 0.0 -1.196961 -1.909887 0.436464
W3 W4 v0 y
0 0.936799 -0.174390 True 12.717473
1 -0.040246 -1.029646 True 15.072868
2 -1.921820 0.121284 True -9.638836
3 1.963276 -1.014058 True 5.584867
4 -0.035781 -0.435584 True -2.168388
#############################################################################################################
Create the CausalModels
[29]:
models = []
for data in datasets:
model = CausalModel(
data = data['df'],
treatment = data['treatment_name'],
outcome = data['outcome_name'],
graph = data['gml_graph']
)
models.append(model)
View Models
[30]:
model.view_model()
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
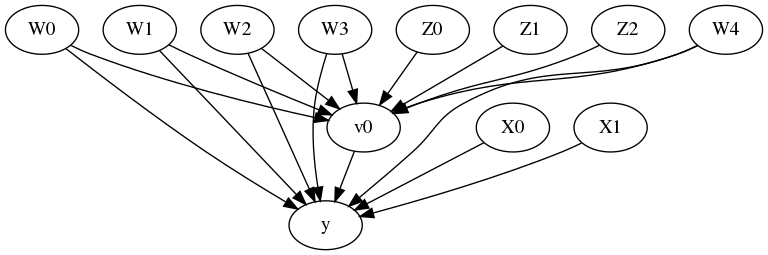
Identify Effect
[31]:
identified_estimands = []
for model in models:
identified_estimand = model.identify_effect(proceed_when_unidentifiable=True)
identified_estimands.append(identified_estimand)
Identified Estimands
[32]:
estimand_count = 1
for estimand in identified_estimands:
print("####### Identified Estimand {}#####################################################################################".format(estimand_count))
print(estimand)
print("###################################################################################################################")
estimand_count += 1
####### Identified Estimand 1#####################################################################################
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(Expectation(y|W0,W1,W4,W3,W2))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W0,W1,W4,W3,W2,U) = P(y|v0,W0,W1,W4,W3,W2)
### Estimand : 2
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z1, Z0, Z2])*Derivative([v0], [Z1, Z0, Z2])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z1,Z0,Z2})
Estimand assumption 2, Exclusion: If we remove {Z1,Z0,Z2}→{v0}, then ¬({Z1,Z0,Z2}→y)
### Estimand : 3
Estimand name: frontdoor
No such variable(s) found!
###################################################################################################################
Estimate Effect
[33]:
estimate_list = []
for i in range(len(identified_estimands)):
for j in range(len(estimator_list)):
estimate = model.estimate_effect(
identified_estimands[i],
method_name=estimator_list[j],
method_params=method_params[j]
)
estimate_list.append(estimate)
Estimate Values
[34]:
estimand_count = 1
if inspect_estimates is True:
for estimand in estimate_list:
print("####### Estimand {}#######################################################################################".format(estimand_count))
print("*** Class Name ***")
print()
print(estimand.params['estimator_class'])
print()
print(estimand)
print("########################################################################################################")
print()
estimand_count += 1
####### Estimand 1#######################################################################################
*** Class Name ***
<class 'dowhy.causal_estimators.propensity_score_matching_estimator.PropensityScoreMatchingEstimator'>
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(Expectation(y|W0,W1,W4,W3,W2))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W0,W1,W4,W3,W2,U) = P(y|v0,W0,W1,W4,W3,W2)
## Realized estimand
b: y~v0+W0+W1+W4+W3+W2
Target units: ate
## Estimate
Mean value: 8.974926096306975
########################################################################################################
####### Estimand 2#######################################################################################
*** Class Name ***
<class 'dowhy.causal_estimators.propensity_score_weighting_estimator.PropensityScoreWeightingEstimator'>
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(Expectation(y|W0,W1,W4,W3,W2))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W0,W1,W4,W3,W2,U) = P(y|v0,W0,W1,W4,W3,W2)
## Realized estimand
b: y~v0+W0+W1+W4+W3+W2
Target units: ate
## Estimate
Mean value: 12.408983841921629
########################################################################################################
####### Estimand 3#######################################################################################
*** Class Name ***
<class 'dowhy.causal_estimators.econml.Econml'>
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────(Expectation(y|W0,W1,W4,W3,W2))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W0,W1,W4,W3,W2,U) = P(y|v0,W0,W1,W4,W3,W2)
## Realized estimand
b: y~v0+W0+W1+W4+W3+W2 | X0,X1
Target units: ate
## Estimate
Mean value: 9.858256590293788
Effect estimates: [11.0297145 9.78699228 10.30838788 ... 9.46308525 9.64756645
10.80259596]
########################################################################################################
Refute Estimate
[35]:
refutation_list = []
for estimand in identified_estimands:
for estimate in estimate_list:
for refuter in refuter_list:
ref = model.refute_estimate(estimand, estimate,method_name=refuter)
refutation_list.append(ref)
Refutation Values
[36]:
refuter_count = 1
if inspect_refutations is True:
for refutation in refutation_list:
print("####### Refutation {}#######################################################################################".format(refuter_count))
print("*** Class Name ***")
print()
print(refutation.refutation_type)
print()
print(refutation)
print("########################################################################################################")
print()
refuter_count += 1
####### Refutation 1#######################################################################################
*** Class Name ***
Refute: Bootstrap Sample Dataset
Refute: Bootstrap Sample Dataset
Estimated effect:8.974926096306975
New effect:9.710002131986627
p value:0.25
########################################################################################################
####### Refutation 2#######################################################################################
*** Class Name ***
Refute: Use a subset of data
Refute: Use a subset of data
Estimated effect:8.974926096306975
New effect:9.859343600595292
p value:0.1
########################################################################################################
####### Refutation 3#######################################################################################
*** Class Name ***
Refute: Bootstrap Sample Dataset
Refute: Bootstrap Sample Dataset
Estimated effect:12.408983841921629
New effect:12.497225598094587
p value:0.31
########################################################################################################
####### Refutation 4#######################################################################################
*** Class Name ***
Refute: Use a subset of data
Refute: Use a subset of data
Estimated effect:12.408983841921629
New effect:12.414222770840858
p value:0.46
########################################################################################################
####### Refutation 5#######################################################################################
*** Class Name ***
Refute: Bootstrap Sample Dataset
Refute: Bootstrap Sample Dataset
Estimated effect:9.858256590293788
New effect:9.904506002270809
p value:0.29
########################################################################################################
####### Refutation 6#######################################################################################
*** Class Name ***
Refute: Use a subset of data
Refute: Use a subset of data
Estimated effect:9.858256590293788
New effect:9.896534434335736
p value:0.28
########################################################################################################