Demo for the DoWhy causal API
We show a simple example of adding a causal extension to any dataframe.
[1]:
import dowhy.datasets
import dowhy.api
import numpy as np
import pandas as pd
from statsmodels.api import OLS
[2]:
data = dowhy.datasets.linear_dataset(beta=5,
num_common_causes=1,
num_instruments = 0,
num_samples=1000,
treatment_is_binary=True)
df = data['df']
df['y'] = df['y'] + np.random.normal(size=len(df)) # Adding noise to data. Without noise, the variance in Y|X, Z is zero, and mcmc fails.
#data['dot_graph'] = 'digraph { v ->y;X0-> v;X0-> y;}'
treatment= data["treatment_name"][0]
outcome = data["outcome_name"][0]
common_cause = data["common_causes_names"][0]
df
[2]:
| W0 | v0 | y | |
|---|---|---|---|
| 0 | 0.339059 | False | 1.523297 |
| 1 | 1.009676 | True | 4.361143 |
| 2 | 0.376290 | True | 7.623149 |
| 3 | 0.832195 | True | 6.504141 |
| 4 | 0.585708 | True | 4.155991 |
| ... | ... | ... | ... |
| 995 | -0.560865 | False | -2.036794 |
| 996 | -0.439966 | False | -1.173392 |
| 997 | -1.545073 | False | -2.369035 |
| 998 | 1.565063 | True | 5.896693 |
| 999 | -1.197883 | True | 2.477574 |
1000 rows × 3 columns
[3]:
# data['df'] is just a regular pandas.DataFrame
df.causal.do(x=treatment,
variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
outcome=outcome,
common_causes=[common_cause],
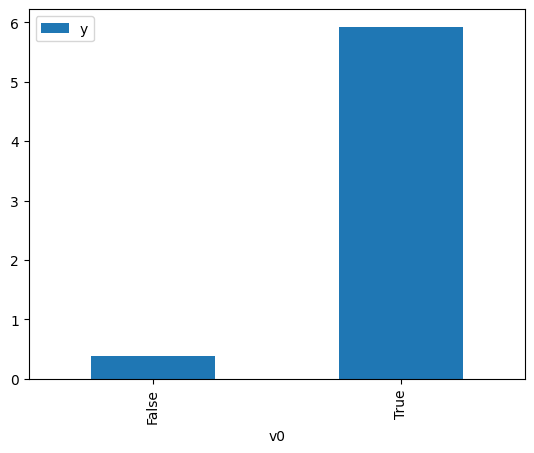
proceed_when_unidentifiable=True).groupby(treatment).mean().plot(y=outcome, kind='bar')
[3]:
<AxesSubplot:xlabel='v0'>
[4]:
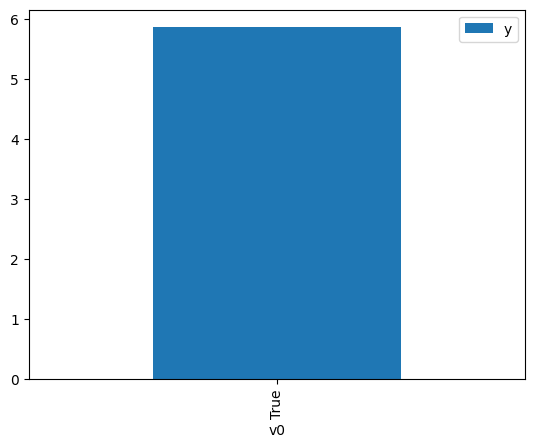
df.causal.do(x={treatment: 1},
variable_types={treatment:'b', outcome: 'c', common_cause: 'c'},
outcome=outcome,
method='weighting',
common_causes=[common_cause],
proceed_when_unidentifiable=True).groupby(treatment).mean().plot(y=outcome, kind='bar')
[4]:
<AxesSubplot:xlabel='v0'>
[5]:
cdf_1 = df.causal.do(x={treatment: 1},
variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
outcome=outcome,
dot_graph=data['dot_graph'],
proceed_when_unidentifiable=True)
cdf_0 = df.causal.do(x={treatment: 0},
variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
outcome=outcome,
dot_graph=data['dot_graph'],
proceed_when_unidentifiable=True)
[6]:
cdf_0
[6]:
| W0 | v0 | y | propensity_score | weight | |
|---|---|---|---|---|---|
| 0 | -0.370839 | False | -1.426270 | 0.668533 | 1.495812 |
| 1 | 1.956810 | False | 1.876996 | 0.017484 | 57.195309 |
| 2 | -0.382916 | False | -1.248201 | 0.673950 | 1.483791 |
| 3 | 0.924422 | False | 1.606464 | 0.126667 | 7.894687 |
| 4 | 0.789872 | False | 1.731581 | 0.160123 | 6.245181 |
| ... | ... | ... | ... | ... | ... |
| 995 | 1.518796 | False | 2.492069 | 0.041540 | 24.073284 |
| 996 | 1.617724 | False | 3.848876 | 0.034233 | 29.211278 |
| 997 | 1.956810 | False | 1.876996 | 0.017484 | 57.195309 |
| 998 | -0.185325 | False | -0.376236 | 0.580432 | 1.722855 |
| 999 | 0.177932 | False | 0.086486 | 0.398028 | 2.512383 |
1000 rows × 5 columns
[7]:
cdf_1
[7]:
| W0 | v0 | y | propensity_score | weight | |
|---|---|---|---|---|---|
| 0 | -0.592847 | True | 3.291838 | 0.239989 | 4.166851 |
| 1 | 1.404890 | True | 4.027509 | 0.948201 | 1.054629 |
| 2 | 0.727954 | True | 5.849403 | 0.822222 | 1.216216 |
| 3 | -0.582116 | True | 4.759021 | 0.243990 | 4.098536 |
| 4 | -0.085492 | True | 4.919241 | 0.469623 | 2.129369 |
| ... | ... | ... | ... | ... | ... |
| 995 | 0.064974 | True | 4.467355 | 0.545902 | 1.831831 |
| 996 | 0.821375 | True | 3.852592 | 0.848300 | 1.178828 |
| 997 | 1.791186 | True | 6.668863 | 0.975690 | 1.024916 |
| 998 | -0.507771 | True | 3.795654 | 0.272923 | 3.664033 |
| 999 | 0.393533 | True | 5.167014 | 0.700954 | 1.426627 |
1000 rows × 5 columns
Comparing the estimate to Linear Regression
First, estimating the effect using the causal data frame, and the 95% confidence interval.
[8]:
(cdf_1['y'] - cdf_0['y']).mean()
[8]:
$\displaystyle 5.39681422096609$
[9]:
1.96*(cdf_1['y'] - cdf_0['y']).std() / np.sqrt(len(df))
[9]:
$\displaystyle 0.134680784526509$
Comparing to the estimate from OLS.
[10]:
model = OLS(np.asarray(df[outcome]), np.asarray(df[[common_cause, treatment]], dtype=np.float64))
result = model.fit()
result.summary()
[10]:
| Dep. Variable: | y | R-squared (uncentered): | 0.966 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared (uncentered): | 0.966 |
| Method: | Least Squares | F-statistic: | 1.407e+04 |
| Date: | Wed, 14 Sep 2022 | Prob (F-statistic): | 0.00 |
| Time: | 19:25:36 | Log-Likelihood: | -1439.7 |
| No. Observations: | 1000 | AIC: | 2883. |
| Df Residuals: | 998 | BIC: | 2893. |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| x1 | 1.2791 | 0.039 | 32.390 | 0.000 | 1.202 | 1.357 |
| x2 | 5.0288 | 0.056 | 89.202 | 0.000 | 4.918 | 5.139 |
| Omnibus: | 3.317 | Durbin-Watson: | 1.975 |
|---|---|---|---|
| Prob(Omnibus): | 0.190 | Jarque-Bera (JB): | 3.386 |
| Skew: | 0.130 | Prob(JB): | 0.184 |
| Kurtosis: | 2.884 | Cond. No. | 2.74 |
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.