Estimating effect of multiple treatments
[1]:
import numpy as np
import pandas as pd
import logging
import dowhy
from dowhy import CausalModel
import dowhy.datasets
import econml
import warnings
warnings.filterwarnings('ignore')
[7]:
data = dowhy.datasets.linear_dataset(10, num_common_causes=4, num_samples=10000,
num_instruments=0, num_effect_modifiers=2,
num_treatments=2,
treatment_is_binary=False,
num_discrete_common_causes=2,
num_discrete_effect_modifiers=0,
one_hot_encode=False)
df=data['df']
df.head()
[7]:
| X0 | X1 | W0 | W1 | W2 | W3 | v0 | v1 | y | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1.915092 | 1.620087 | -0.734004 | 1.166135 | 1 | 1 | 4.812868 | 6.143449 | 315.635386 |
| 1 | 0.002147 | 0.669278 | -0.488148 | 1.662905 | 0 | 0 | 2.241058 | -0.507441 | 20.008368 |
| 2 | 0.248668 | 0.744331 | 0.395333 | 0.363403 | 1 | 1 | 8.223679 | 9.169402 | 322.803160 |
| 3 | 1.391820 | 0.685058 | 2.196834 | -0.031341 | 1 | 2 | 13.784811 | 16.208969 | 1188.634520 |
| 4 | 0.978381 | 0.656576 | 0.686080 | 0.260394 | 2 | 1 | 12.353938 | 13.503698 | 785.596373 |
[8]:
model = CausalModel(data=data["df"],
treatment=data["treatment_name"], outcome=data["outcome_name"],
graph=data["gml_graph"])
INFO:dowhy.causal_model:Model to find the causal effect of treatment ['v0', 'v1'] on outcome ['y']
[9]:
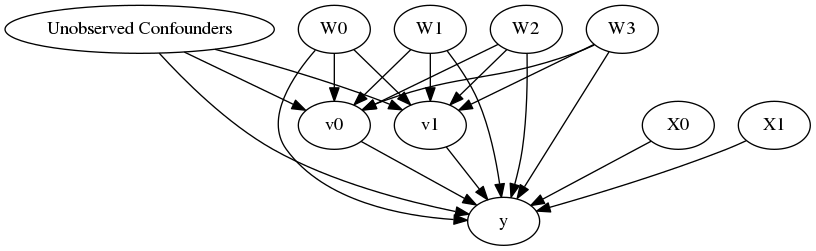
model.view_model()
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
[10]:
identified_estimand= model.identify_effect()
print(identified_estimand)
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['W0', 'Unobserved Confounders', 'W1', 'W2', 'W3']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
WARN: Do you want to continue by ignoring any unobserved confounders? (use proceed_when_unidentifiable=True to disable this prompt) [y/n] y
INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:[]
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────────(Expectation(y|W0,W1,W2,W3))
d[v₀ v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W0,W1,W2,W3,U) = P(y|v0,v1,W0,W1,W2,W3)
### Estimand : 2
Estimand name: iv
No such variable found!
Linear model
Let us first see an example for a linear model. The control_value and treatment_value can be provided as a tuple/list when the treatment is multi-dimensional.
The interpretation is change in y when v0 and v1 are changed from (0,0) to (1,1).
[16]:
linear_estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.linear_regression",
control_value=(0,0),
treatment_value=(1,1),
method_params={'need_conditional_estimates': False})
print(linear_estimate)
INFO:dowhy.causal_estimator:INFO: Using Linear Regression Estimator
INFO:dowhy.causal_estimator:b: y~v0+v1+W0+W1+W2+W3+v0*X0+v0*X1+v1*X0+v1*X1
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────────(Expectation(y|W0,W1,W2,W3))
d[v₀ v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W0,W1,W2,W3,U) = P(y|v0,v1,W0,W1,W2,W3)
### Estimand : 2
Estimand name: iv
No such variable found!
## Realized estimand
b: y~v0+v1+W0+W1+W2+W3+v0*X0+v0*X1+v1*X0+v1*X1
Target units: ate
## Estimate
Mean value: 90.33055385892129
You can estimate conditional effects, based on effect modifiers.
[18]:
linear_estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.linear_regression",
control_value=(0,0),
treatment_value=(1,1))
print(linear_estimate)
INFO:dowhy.causal_estimator:INFO: Using Linear Regression Estimator
INFO:dowhy.causal_estimator:b: y~v0+v1+W0+W1+W2+W3+v0*X0+v0*X1+v1*X0+v1*X1
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
d
─────────(Expectation(y|W0,W1,W2,W3))
d[v₀ v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W0,W1,W2,W3,U) = P(y|v0,v1,W0,W1,W2,W3)
### Estimand : 2
Estimand name: iv
No such variable found!
## Realized estimand
b: y~v0+v1+W0+W1+W2+W3+v0*X0+v0*X1+v1*X0+v1*X1
Target units: ate
## Estimate
Mean value: 90.33055385892129
### Conditional Estimates
__categorical__X0 __categorical__X1
(-2.629, 0.14] (-2.936, 0.0176] -3.709237
(0.0176, 0.586] 25.191433
(0.586, 1.084] 43.708158
(1.084, 1.661] 61.782760
(1.661, 4.444] 90.521027
(0.14, 0.72] (-2.936, 0.0176] 24.438689
(0.0176, 0.586] 54.299181
(0.586, 1.084] 72.005026
(1.084, 1.661] 90.203724
(1.661, 4.444] 119.455480
(0.72, 1.232] (-2.936, 0.0176] 41.988317
(0.0176, 0.586] 72.977085
(0.586, 1.084] 90.270855
(1.084, 1.661] 108.403973
(1.661, 4.444] 136.661504
(1.232, 1.845] (-2.936, 0.0176] 58.596700
(0.0176, 0.586] 90.604757
(0.586, 1.084] 108.531656
(1.084, 1.661] 126.376825
(1.661, 4.444] 156.005501
(1.845, 4.73] (-2.936, 0.0176] 90.504006
(0.0176, 0.586] 120.364554
(0.586, 1.084] 137.619648
(1.084, 1.661] 155.753611
(1.661, 4.444] 185.702174
dtype: float64
More methods
You can also use methods from EconML or CausalML libraries that support multiple treatments. You can look at examples from the conditional effect notebook: https://microsoft.github.io/dowhy/example_notebooks/dowhy-conditional-treatment-effects.html
Propensity-based methods do not support multiple treatments currently.