Estimating effect of multiple treatments
[1]:
import numpy as np
import pandas as pd
import logging
import dowhy
from dowhy import CausalModel
import dowhy.datasets
import econml
import warnings
warnings.filterwarnings('ignore')
[2]:
data = dowhy.datasets.linear_dataset(10, num_common_causes=4, num_samples=10000,
num_instruments=0, num_effect_modifiers=2,
num_treatments=2,
treatment_is_binary=False,
num_discrete_common_causes=2,
num_discrete_effect_modifiers=0,
one_hot_encode=False)
df=data['df']
df.head()
[2]:
| X0 | X1 | W0 | W1 | W2 | W3 | v0 | v1 | y | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | -0.124175 | -0.186845 | -1.724130 | 1.431111 | 2 | 0 | -3.091154 | -1.415971 | -43.825403 |
| 1 | -2.842135 | -1.132385 | 0.384155 | 0.486554 | 1 | 2 | 10.143039 | 2.395090 | -127.314940 |
| 2 | -0.391815 | 0.958121 | 1.138954 | -1.643331 | 1 | 1 | 4.643046 | -0.536156 | 39.479516 |
| 3 | -0.873968 | -1.297226 | -0.376918 | -1.489406 | 1 | 3 | 6.786418 | -1.775266 | 146.484902 |
| 4 | -2.925996 | 0.066473 | -1.691236 | -0.863161 | 1 | 1 | -3.386294 | -6.167120 | -221.136065 |
[3]:
model = CausalModel(data=data["df"],
treatment=data["treatment_name"], outcome=data["outcome_name"],
graph=data["gml_graph"])
INFO:dowhy.causal_model:Model to find the causal effect of treatment ['v0', 'v1'] on outcome ['y']
[4]:
model.view_model()
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
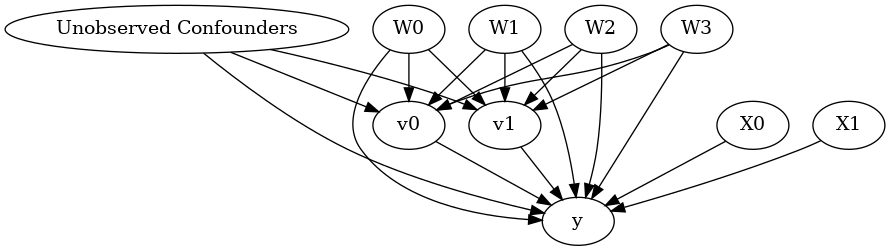
[5]:
identified_estimand= model.identify_effect(proceed_when_unidentifiable=True)
print(identified_estimand)
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
INFO:dowhy.causal_identifier:Continuing by ignoring these unobserved confounders because proceed_when_unidentifiable flag is True.
INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:[]
INFO:dowhy.causal_identifier:Frontdoor variables for treatment and outcome:[]
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor1
Estimand expression:
d
─────────(Expectation(y|W2,W0,W1,W3))
d[v₀ v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W2,W0,W1,W3,U) = P(y|v0,v1,W2,W0,W1,W3)
### Estimand : 2
Estimand name: backdoor2
Estimand expression:
d
─────────(Expectation(y|W2,W0,X0,W1,W3))
d[v₀ v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W2,W0,X0,W1,W3,U) = P(y|v0,v1,W2,W0,X0,W1,W3)
### Estimand : 3
Estimand name: backdoor3
Estimand expression:
d
─────────(Expectation(y|W2,W0,W1,X1,W3))
d[v₀ v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W2,W0,W1,X1,W3,U) = P(y|v0,v1,W2,W0,W1,X1,W3)
### Estimand : 4
Estimand name: backdoor4 (Default)
Estimand expression:
d
─────────(Expectation(y|W2,W0,X0,W1,X1,W3))
d[v₀ v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W2,W0,X0,W1,X1,W3,U) = P(y|v0,v1,W2,W0,X0,W1,X1,W3)
### Estimand : 5
Estimand name: iv
No such variable found!
### Estimand : 6
Estimand name: frontdoor
No such variable found!
Linear model
Let us first see an example for a linear model. The control_value and treatment_value can be provided as a tuple/list when the treatment is multi-dimensional.
The interpretation is change in y when v0 and v1 are changed from (0,0) to (1,1).
[6]:
linear_estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.linear_regression",
control_value=(0,0),
treatment_value=(1,1),
method_params={'need_conditional_estimates': False})
print(linear_estimate)
INFO:dowhy.causal_estimator:b: y~v0+v1+W2+W0+X0+W1+X1+W3+v0*X0+v0*X1+v1*X0+v1*X1
INFO:dowhy.causal_estimator:INFO: Using Linear Regression Estimator
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
## Realized estimand
b: y~v0+v1+W2+W0+X0+W1+X1+W3+v0*X0+v0*X1+v1*X0+v1*X1
Target units: ate
## Estimate
Mean value: 12.451340507824497
You can estimate conditional effects, based on effect modifiers.
[7]:
linear_estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.linear_regression",
control_value=(0,0),
treatment_value=(1,1))
print(linear_estimate)
INFO:dowhy.causal_estimator:b: y~v0+v1+W2+W0+X0+W1+X1+W3+v0*X0+v0*X1+v1*X0+v1*X1
INFO:dowhy.causal_estimator:INFO: Using Linear Regression Estimator
*** Causal Estimate ***
## Identified estimand
Estimand type: nonparametric-ate
## Realized estimand
b: y~v0+v1+W2+W0+X0+W1+X1+W3+v0*X0+v0*X1+v1*X0+v1*X1
Target units: ate
## Estimate
Mean value: 12.451340507824497
### Conditional Estimates
__categorical__X0 __categorical__X1
(-4.421, -1.185] (-4.422000000000001, -1.353] -12.354725
(-1.353, -0.786] -2.843684
(-0.786, -0.28] 2.985760
(-0.28, 0.323] 9.293470
(0.323, 3.331] 18.744462
(-1.185, -0.591] (-4.422000000000001, -1.353] -6.742414
(-1.353, -0.786] 2.913217
(-0.786, -0.28] 8.734612
(-0.28, 0.323] 14.918588
(0.323, 3.331] 24.805595
(-0.591, -0.0849] (-4.422000000000001, -1.353] -3.542468
(-1.353, -0.786] 6.433089
(-0.786, -0.28] 12.504268
(-0.28, 0.323] 18.370863
(0.323, 3.331] 28.043426
(-0.0849, 0.518] (-4.422000000000001, -1.353] 0.603679
(-1.353, -0.786] 10.049479
(-0.786, -0.28] 15.792282
(-0.28, 0.323] 22.067883
(0.323, 3.331] 31.751841
(0.518, 3.039] (-4.422000000000001, -1.353] 6.619841
(-1.353, -0.786] 15.691690
(-0.786, -0.28] 21.677279
(-0.28, 0.323] 27.377128
(0.323, 3.331] 37.370099
dtype: float64
More methods
You can also use methods from EconML or CausalML libraries that support multiple treatments. You can look at examples from the conditional effect notebook: https://microsoft.github.io/dowhy/example_notebooks/dowhy-conditional-treatment-effects.html
Propensity-based methods do not support multiple treatments currently.