DoWhy: Different estimation methods for causal inference

This is a quick introduction to the DoWhy causal inference library. We will load in a sample dataset and use different methods for estimating the causal effect of a (pre-specified)treatment variable on a (pre-specified) outcome variable.

First, let us add the required path for Python to find the DoWhy code and load all required packages

[1]:

import os, sys
sys.path.append(os.path.abspath("../../../"))

[2]:

import numpy as np
import pandas as pd
import logging

import dowhy
from dowhy import CausalModel
import dowhy.datasets

Now, let us load a dataset. For simplicity, we simulate a dataset with linear relationships between common causes and treatment, and common causes and outcome.

Beta is the true causal effect.

[3]:

data = dowhy.datasets.linear_dataset(beta=10,
        num_common_causes=5,
        num_instruments = 2,
        num_treatments=1,
        num_samples=10000,
        treatment_is_binary=True,
        outcome_is_binary=False)
df = data["df"]
df

[3]:

	Z0	Z1	W0	W1	W2	W3	W4	v0	y
0	1.0	0.856829	0.871424	-0.792461	-0.336331	0.386621	-0.068865	True	9.124501
1	1.0	0.491077	0.197358	-0.505399	-0.424140	0.367762	0.168461	True	8.622930
2	1.0	0.665795	0.945841	-0.288969	0.274395	-1.312587	2.382897	True	17.977266
3	1.0	0.902905	1.268346	-0.059530	0.315513	-0.932715	-1.360252	True	8.367090
4	1.0	0.104740	-1.342788	-1.935350	-0.649980	-0.852453	0.843568	True	-1.326686
...	...	...	...	...	...	...	...	...	...
9995	1.0	0.577368	1.846929	0.755214	-2.979011	1.525415	-0.225743	True	9.653687
9996	1.0	0.131065	1.880914	-1.314365	-0.538280	-0.303415	0.863559	True	11.305263
9997	1.0	0.739417	-0.974042	-0.707890	-0.028049	-1.371608	0.100693	True	2.620035
9998	1.0	0.489953	-0.363797	-0.590689	-1.905395	-0.374315	0.622429	True	1.844830
9999	1.0	0.484942	1.118425	-0.414818	-1.112958	0.608269	1.865714	True	15.116874

10000 rows × 9 columns

Note that we are using a pandas dataframe to load the data.

Identifying the causal estimand

We now input a causal graph in the DOT graph format.

[4]:

# With graph
model=CausalModel(
        data = df,
        treatment=data["treatment_name"],
        outcome=data["outcome_name"],
        graph=data["gml_graph"],
        instruments=data["instrument_names"],
        logging_level = logging.INFO
        )

INFO:dowhy.causal_model:Model to find the causal effect of treatment ['v0'] on outcome ['y']

[5]:

model.view_model()

[6]:

from IPython.display import Image, display
display(Image(filename="causal_model.png"))

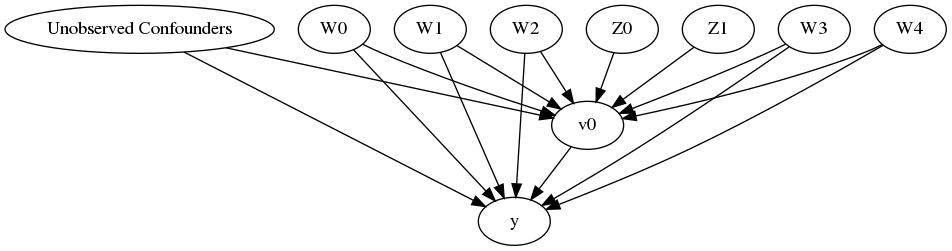
../_images/example_notebooks_dowhy_estimation_methods_10_0.png

We get a causal graph. Now identification and estimation is done.

[7]:

identified_estimand = model.identify_effect()
print(identified_estimand)

INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['W1', 'W4', 'W0', 'W2', 'Unobserved Confounders', 'W3']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.

WARN: Do you want to continue by ignoring any unobserved confounders? (use proceed_when_unidentifiable=True to disable this prompt) [y/n] y

INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:['Z0', 'Z1']

Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
  d
─────(Expectation(y|W1,W4,W0,W2,W3))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W4,W0,W2,W3,U) = P(y|v0,W1,W4,W0,W2,W3)
### Estimand : 2
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z0, Z1])*Derivative([v0], [Z0, Z1])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)

Method 1: Regression

Use linear regression.

[8]:

causal_estimate_reg = model.estimate_effect(identified_estimand,
        method_name="backdoor.linear_regression",
        test_significance=True)
print(causal_estimate_reg)
print("Causal Estimate is " + str(causal_estimate_reg.value))

INFO:dowhy.causal_estimator:INFO: Using Linear Regression Estimator
INFO:dowhy.causal_estimator:b: y~v0+W1+W4+W0+W2+W3

*** Causal Estimate ***

## Target estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
  d
─────(Expectation(y|W1,W4,W0,W2,W3))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W4,W0,W2,W3,U) = P(y|v0,W1,W4,W0,W2,W3)
### Estimand : 2
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z0, Z1])*Derivative([v0], [Z0, Z1])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)

## Realized estimand
b: y~v0+W1+W4+W0+W2+W3
## Estimate
Value: 10.000000000000021

## Statistical Significance
p-value: <0.001

Causal Estimate is 10.000000000000021

Method 2: Stratification

We will be using propensity scores to stratify units in the data.

[9]:

causal_estimate_strat = model.estimate_effect(identified_estimand,
                                              method_name="backdoor.propensity_score_stratification",
                                              target_units="att")
print(causal_estimate_strat)
print("Causal Estimate is " + str(causal_estimate_strat.value))

INFO:dowhy.causal_estimator:INFO: Using Propensity Score Stratification Estimator
INFO:dowhy.causal_estimator:b: y~v0+W1+W4+W0+W2+W3
/home/amshar/python-environments/vpy36/lib/python3.6/site-packages/sklearn/utils/validation.py:744: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
  y = column_or_1d(y, warn=True)

*** Causal Estimate ***

## Target estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
  d
─────(Expectation(y|W1,W4,W0,W2,W3))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W4,W0,W2,W3,U) = P(y|v0,W1,W4,W0,W2,W3)
### Estimand : 2
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z0, Z1])*Derivative([v0], [Z0, Z1])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)

## Realized estimand
b: y~v0+W1+W4+W0+W2+W3
## Estimate
Value: 10.173499320316472

Causal Estimate is 10.173499320316472

Method 3: Matching

We will be using propensity scores to match units in the data.

[10]:

causal_estimate_match = model.estimate_effect(identified_estimand,
                                              method_name="backdoor.propensity_score_matching",
                                              target_units="atc")
print(causal_estimate_match)
print("Causal Estimate is " + str(causal_estimate_match.value))

INFO:dowhy.causal_estimator:INFO: Using Propensity Score Matching Estimator
INFO:dowhy.causal_estimator:b: y~v0+W1+W4+W0+W2+W3
/home/amshar/python-environments/vpy36/lib/python3.6/site-packages/sklearn/utils/validation.py:744: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
  y = column_or_1d(y, warn=True)
/mnt/c/Users/amshar/code/dowhy/dowhy/causal_estimators/propensity_score_matching_estimator.py:62: FutureWarning: `item` has been deprecated and will be removed in a future version
  control_outcome = control.iloc[indices[i]][self._outcome_name].item()

*** Causal Estimate ***

## Target estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
  d
─────(Expectation(y|W1,W4,W0,W2,W3))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W4,W0,W2,W3,U) = P(y|v0,W1,W4,W0,W2,W3)
### Estimand : 2
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z0, Z1])*Derivative([v0], [Z0, Z1])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)

## Realized estimand
b: y~v0+W1+W4+W0+W2+W3
## Estimate
Value: 10.036816324727294

Causal Estimate is 10.036816324727294

/mnt/c/Users/amshar/code/dowhy/dowhy/causal_estimators/propensity_score_matching_estimator.py:77: FutureWarning: `item` has been deprecated and will be removed in a future version
  treated_outcome = treated.iloc[indices[i]][self._outcome_name].item()

Method 4: Weighting

We will be using (inverse) propensity scores to assign weights to units in the data. DoWhy supports a few different weighting schemes: 1. Vanilla Inverse Propensity Score weighting (IPS) (weighting_scheme=“ips_weight”) 2. Self-normalized IPS weighting (also known as the Hajek estimator) (weighting_scheme=“ips_normalized_weight”) 3. Stabilized IPS weighting (weighting_scheme = “ips_stabilized_weight”)

[11]:

causal_estimate_ipw = model.estimate_effect(identified_estimand,
                                            method_name="backdoor.propensity_score_weighting",
                                            target_units = "ate",
                                            method_params={"weighting_scheme":"ips_weight"})
print(causal_estimate_ipw)
print("Causal Estimate is " + str(causal_estimate_ipw.value))

INFO:dowhy.causal_estimator:INFO: Using Propensity Score Weighting Estimator
INFO:dowhy.causal_estimator:b: y~v0+W1+W4+W0+W2+W3

*** Causal Estimate ***

## Target estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
  d
─────(Expectation(y|W1,W4,W0,W2,W3))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W4,W0,W2,W3,U) = P(y|v0,W1,W4,W0,W2,W3)
### Estimand : 2
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z0, Z1])*Derivative([v0], [Z0, Z1])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)

## Realized estimand
b: y~v0+W1+W4+W0+W2+W3
## Estimate
Value: 10.722320441623154

Causal Estimate is 10.722320441623154

/home/amshar/python-environments/vpy36/lib/python3.6/site-packages/sklearn/utils/validation.py:744: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
  y = column_or_1d(y, warn=True)

Method 5: Instrumental Variable

We will be using the Wald estimator for the provided instrumental variable.

[12]:

causal_estimate_iv = model.estimate_effect(identified_estimand,
        method_name="iv.instrumental_variable", method_params = {'iv_instrument_name': 'Z0'})
print(causal_estimate_iv)
print("Causal Estimate is " + str(causal_estimate_iv.value))

INFO:dowhy.causal_estimator:INFO: Using Instrumental Variable Estimator
INFO:dowhy.causal_estimator:Realized estimand: Wald Estimator
Realized estimand type: nonparametric-ate
Estimand expression:
                                                              -1
Expectation(Derivative(y, Z0))⋅Expectation(Derivative(v0, Z0))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)
Estimand assumption 3, treatment_effect_homogeneity: Each unit's treatment ['v0'] is affected in the same way by common causes of ['v0'] and y
Estimand assumption 4, outcome_effect_homogeneity: Each unit's outcome y is affected in the same way by common causes of ['v0'] and y

*** Causal Estimate ***

## Target estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
  d
─────(Expectation(y|W1,W4,W0,W2,W3))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W4,W0,W2,W3,U) = P(y|v0,W1,W4,W0,W2,W3)
### Estimand : 2
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z0, Z1])*Derivative([v0], [Z0, Z1])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)

## Realized estimand
Realized estimand: Wald Estimator
Realized estimand type: nonparametric-ate
Estimand expression:
                                                              -1
Expectation(Derivative(y, Z0))⋅Expectation(Derivative(v0, Z0))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)
Estimand assumption 3, treatment_effect_homogeneity: Each unit's treatment ['v0'] is affected in the same way by common causes of ['v0'] and y
Estimand assumption 4, outcome_effect_homogeneity: Each unit's outcome y is affected in the same way by common causes of ['v0'] and y

## Estimate
Value: 6.7777521025251435

Causal Estimate is 6.7777521025251435

Method 6: Regression Discontinuity

We will be internally converting this to an equivalent instrumental variables problem.

[13]:

causal_estimate_regdist = model.estimate_effect(identified_estimand,
        method_name="iv.regression_discontinuity",
        method_params={'rd_variable_name':'Z1',
                       'rd_threshold_value':0.5,
                       'rd_bandwidth': 0.1})
print(causal_estimate_regdist)
print("Causal Estimate is " + str(causal_estimate_regdist.value))

INFO:dowhy.causal_estimator:Using Regression Discontinuity Estimator
INFO:dowhy.causal_estimator:
INFO:dowhy.causal_estimator:INFO: Using Instrumental Variable Estimator
INFO:dowhy.causal_estimator:Realized estimand: Wald Estimator
Realized estimand type: nonparametric-ate
Estimand expression:

Expectation(Derivative(y, local_rd_variable))⋅Expectation(Derivative(v0, local

              -1
_rd_variable))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)
Estimand assumption 3, treatment_effect_homogeneity: Each unit's treatment ['local_treatment'] is affected in the same way by common causes of ['local_treatment'] and local_outcome
Estimand assumption 4, outcome_effect_homogeneity: Each unit's outcome local_outcome is affected in the same way by common causes of ['local_treatment'] and local_outcome

      local_rd_variable  local_treatment  local_outcome
1              0.491077             True       8.622930
17             0.526249             True       1.107572
18             0.557455             True       4.576484
24             0.416279             True      -5.730869
25             0.554845             True       1.196812
...                 ...              ...            ...
9974           0.531890             True       1.377569
9982           0.575699             True      14.511282
9995           0.577368             True       9.653687
9998           0.489953             True       1.844830
9999           0.484942             True      15.116874

[1924 rows x 3 columns]
*** Causal Estimate ***

## Target estimand
Estimand type: nonparametric-ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
  d
─────(Expectation(y|W1,W4,W0,W2,W3))
d[v₀]
Estimand assumption 1, Unconfoundedness: If U→{v0} and U→y then P(y|v0,W1,W4,W0,W2,W3,U) = P(y|v0,W1,W4,W0,W2,W3)
### Estimand : 2
Estimand name: iv
Estimand expression:
Expectation(Derivative(y, [Z0, Z1])*Derivative([v0], [Z0, Z1])**(-1))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)

## Realized estimand
Realized estimand: Wald Estimator
Realized estimand type: nonparametric-ate
Estimand expression:

Expectation(Derivative(y, local_rd_variable))⋅Expectation(Derivative(v0, local

              -1
_rd_variable))
Estimand assumption 1, As-if-random: If U→→y then ¬(U →→{Z0,Z1})
Estimand assumption 2, Exclusion: If we remove {Z0,Z1}→{v0}, then ¬({Z0,Z1}→y)
Estimand assumption 3, treatment_effect_homogeneity: Each unit's treatment ['local_treatment'] is affected in the same way by common causes of ['local_treatment'] and local_outcome
Estimand assumption 4, outcome_effect_homogeneity: Each unit's outcome local_outcome is affected in the same way by common causes of ['local_treatment'] and local_outcome

## Estimate
Value: 22.999383345332262

Causal Estimate is 22.999383345332262