Demo for the DoWhy causal API

We show a simple example of adding a causal extension to any dataframe.

import os, sys
sys.path.append(os.path.abspath("../../../"))

import dowhy.datasets
import dowhy.api

import numpy as np
import pandas as pd

from statsmodels.api import OLS

data = dowhy.datasets.linear_dataset(beta=5,
        num_common_causes=1,
        num_instruments = 0,
        num_samples=1000,
        treatment_is_binary=True)
df = data['df']
df['y'] = df['y'] + np.random.normal(size=len(df)) # Adding noise to data. Without noise, the variance in Y|X, Z is zero, and mcmc fails.
#data['dot_graph'] = 'digraph { v ->y;X0-> v;X0-> y;}'

treatment= data["treatment_name"][0]
outcome = data["outcome_name"][0]
common_cause = data["common_causes_names"][0]
df

	W0	v0	y
0	0.230046	False	0.328777
1	-0.625509	True	3.794958
2	-2.600417	False	-5.214096
3	0.146942	False	1.361876
4	-0.919551	False	-2.228864
...	...	...	...
995	-0.063647	False	0.117779
996	-1.962547	False	-4.034488
997	-0.089728	True	5.780041
998	-0.334302	True	3.872871
999	-2.410448	False	-4.524930

1000 rows × 3 columns

# data['df'] is just a regular pandas.DataFrame
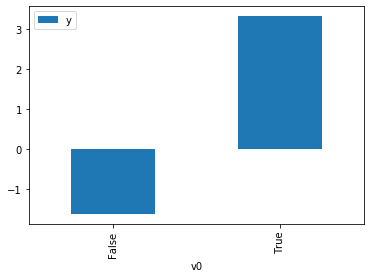
df.causal.do(x=treatment,
                     variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
                     outcome=outcome,
                     common_causes=[common_cause]).groupby(treatment).mean().plot(y=outcome, kind='bar')

WARNING:dowhy.causal_model:Causal Graph not provided. DoWhy will construct a graph based on data inputs.
INFO:dowhy.causal_graph:If this is observed data (not from a randomized experiment), there might always be missing confounders. Adding a node named "Unobserved Confounders" to reflect this.
INFO:dowhy.causal_model:Model to find the causal effect of treatment ['v0'] on outcome ['y']
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['W0', 'U']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.

WARN: Do you want to continue by ignoring any unobserved confounders? (use proceed_when_unidentifiable=True to disable this prompt) [y/n] y

INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:[]
INFO:dowhy.do_sampler:Using WeightingSampler for do sampling.
INFO:dowhy.do_sampler:Caution: do samplers assume iid data.

<matplotlib.axes._subplots.AxesSubplot at 0x7f0f4a609e80>

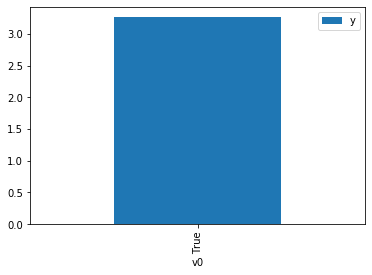
df.causal.do(x={treatment: 1},
              variable_types={treatment:'b', outcome: 'c', common_cause: 'c'},
              outcome=outcome,
              method='weighting',
              common_causes=[common_cause],
              proceed_when_unidentifiable=True).groupby(treatment).mean().plot(y=outcome, kind='bar')

WARNING:dowhy.causal_model:Causal Graph not provided. DoWhy will construct a graph based on data inputs.
INFO:dowhy.causal_graph:If this is observed data (not from a randomized experiment), there might always be missing confounders. Adding a node named "Unobserved Confounders" to reflect this.
INFO:dowhy.causal_model:Model to find the causal effect of treatment ['v0'] on outcome ['y']
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['W0', 'U']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
INFO:dowhy.causal_identifier:Continuing by ignoring these unobserved confounders because proceed_when_unidentifiable flag is True.
INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:[]
INFO:dowhy.do_sampler:Using WeightingSampler for do sampling.
INFO:dowhy.do_sampler:Caution: do samplers assume iid data.

<matplotlib.axes._subplots.AxesSubplot at 0x7f0f48316358>

cdf_1 = df.causal.do(x={treatment: 1},
              variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
              outcome=outcome,
              dot_graph=data['dot_graph'],
              proceed_when_unidentifiable=True)

cdf_0 = df.causal.do(x={treatment: 0},
              variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
              outcome=outcome,
              dot_graph=data['dot_graph'],
              proceed_when_unidentifiable=True)

INFO:dowhy.causal_model:Model to find the causal effect of treatment ['v0'] on outcome ['y']
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['W0', 'U']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
INFO:dowhy.causal_identifier:Continuing by ignoring these unobserved confounders because proceed_when_unidentifiable flag is True.
INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:[]
INFO:dowhy.do_sampler:Using WeightingSampler for do sampling.
INFO:dowhy.do_sampler:Caution: do samplers assume iid data.
INFO:dowhy.causal_model:Model to find the causal effect of treatment ['v0'] on outcome ['y']
INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['W0', 'U']
WARNING:dowhy.causal_identifier:If this is observed data (not from a randomized experiment), there might always be missing confounders. Causal effect cannot be identified perfectly.
INFO:dowhy.causal_identifier:Continuing by ignoring these unobserved confounders because proceed_when_unidentifiable flag is True.
INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:[]
INFO:dowhy.do_sampler:Using WeightingSampler for do sampling.
INFO:dowhy.do_sampler:Caution: do samplers assume iid data.

cdf_0

	W0	v0	y	propensity_score	weight
0	-0.583286	False	-2.456860	0.574597	1.740350
1	-1.853274	False	-3.699267	0.754520	1.325346
2	-1.530711	False	-4.384006	0.713824	1.400906
3	-0.036469	False	-2.269524	0.486654	2.054847
4	-1.749115	False	-3.311137	0.741816	1.348043
...	...	...	...	...	...
995	-1.227516	False	-0.875867	0.672107	1.487859
996	-0.405553	False	-1.427872	0.546258	1.830637
997	0.230046	False	0.328777	0.443752	2.253509
998	-2.157752	False	-4.830362	0.789181	1.267136
999	-0.453149	False	-2.167928	0.553884	1.805431

1000 rows × 5 columns

cdf_1

	W0	v0	y	propensity_score	weight
0	-0.229733	True	4.754793	0.482075	2.074366
1	-0.238390	True	4.487643	0.480676	2.080404
2	-2.161507	True	-1.700668	0.210415	4.752520
3	-1.639879	True	2.173829	0.271959	3.677028
4	0.030840	True	4.465655	0.524224	1.907580
...	...	...	...	...	...
995	-1.688769	True	2.404017	0.265737	3.763121
996	-0.910527	True	2.528176	0.374608	2.669460
997	-2.838431	True	-0.226373	0.146704	6.816457
998	0.429132	True	6.865883	0.587791	1.701285
999	-1.509348	True	2.153207	0.289010	3.460088

1000 rows × 5 columns

Comparing the estimate to Linear Regression

First, estimating the effect using the causal data frame, and the 95% confidence interval.

(cdf_1['y'] - cdf_0['y']).mean()

$\displaystyle 5.006194579687894$

1.96*(cdf_1['y'] - cdf_0['y']).std() / np.sqrt(len(df))

$\displaystyle 0.2245958282589085$

Comparing to the estimate from OLS.

model = OLS(np.asarray(df[outcome]), np.asarray(df[[common_cause, treatment]], dtype=np.float64))
result = model.fit()
result.summary()

OLS Regression Results

Dep. Variable:	y	R-squared (uncentered):	0.938
Model:	OLS	Adj. R-squared (uncentered):	0.938
Method:	Least Squares	F-statistic:	7544.
Date:	Tue, 07 Jan 2020	Prob (F-statistic):	0.00
Time:	11:54:35	Log-Likelihood:	-1408.7
No. Observations:	1000	AIC:	2821.
Df Residuals:	998	BIC:	2831.
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
x1	2.2679	0.025	89.049	0.000	2.218	2.318
x2	5.0091	0.050	100.297	0.000	4.911	5.107

Omnibus:	2.664	Durbin-Watson:	2.034
Prob(Omnibus):	0.264	Jarque-Bera (JB):	2.431
Skew:	-0.049	Prob(JB):	0.297
Kurtosis:	2.779	Cond. No.	2.03

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.