Estimating effect of multiple treatments

from dowhy import CausalModel
import dowhy.datasets

import warnings
warnings.filterwarnings('ignore')

data = dowhy.datasets.linear_dataset(10, num_common_causes=4, num_samples=10000,
                                     num_instruments=0, num_effect_modifiers=2,
                                     num_treatments=2,
                                     treatment_is_binary=False,
                                     num_discrete_common_causes=2,
                                     num_discrete_effect_modifiers=0,
                                     one_hot_encode=False)
df=data['df']
df.head()

	X0	X1	W0	W1	W2	W3	v0	v1	y
0	-0.160726	0.197717	0.168884	0.281044	0	2	7.305433	1.566046	96.418483
1	0.622458	1.749118	1.266611	-0.697390	3	3	22.841898	17.612662	4068.381933
2	-0.507455	0.239130	-0.343174	0.415110	0	2	3.728880	2.577602	59.251898
3	-0.762805	-0.040333	-2.167921	-0.418095	2	1	-3.357920	7.994089	131.406754
4	-1.552625	0.831265	1.186141	-0.322733	2	3	19.853591	15.394102	-437.483542

model = CausalModel(data=data["df"],
                    treatment=data["treatment_name"], outcome=data["outcome_name"],
                    graph=data["gml_graph"])

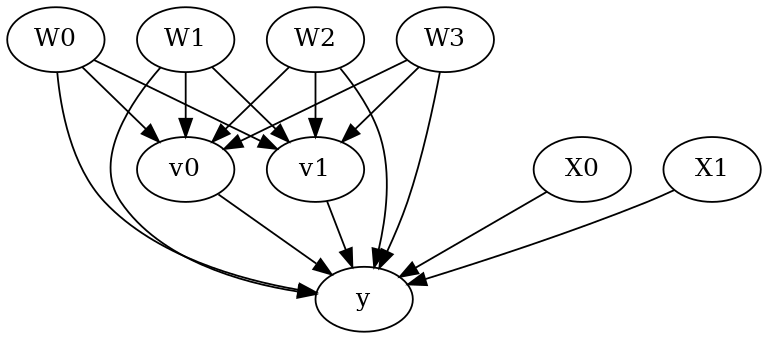
model.view_model()
from IPython.display import Image, display
display(Image(filename="causal_model.png"))

identified_estimand= model.identify_effect(proceed_when_unidentifiable=True)
print(identified_estimand)

Estimand type: EstimandType.NONPARAMETRIC_ATE

### Estimand : 1
Estimand name: backdoor
Estimand expression:
    d
─────────(E[y|W0,W3,W2,W1])
d[v₀  v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W0,W3,W2,W1,U) = P(y|v0,v1,W0,W3,W2,W1)

### Estimand : 2
Estimand name: iv
No such variable(s) found!

### Estimand : 3
Estimand name: frontdoor
No such variable(s) found!

Linear model

Let us first see an example for a linear model. The control_value and treatment_value can be provided as a tuple/list when the treatment is multi-dimensional.

The interpretation is change in y when v0 and v1 are changed from (0,0) to (1,1).

linear_estimate = model.estimate_effect(identified_estimand,
                                        method_name="backdoor.linear_regression",
                                        control_value=(0,0),
                                        treatment_value=(1,1),
                                        method_params={'need_conditional_estimates': False})
print(linear_estimate)

*** Causal Estimate ***

## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE

### Estimand : 1
Estimand name: backdoor
Estimand expression:
    d
─────────(E[y|W0,W3,W2,W1])
d[v₀  v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W0,W3,W2,W1,U) = P(y|v0,v1,W0,W3,W2,W1)

## Realized estimand
b: y~v0+v1+W0+W3+W2+W1+v0*X1+v0*X0+v1*X1+v1*X0
Target units: ate

## Estimate
Mean value: 19.38227351230603

You can estimate conditional effects, based on effect modifiers.

linear_estimate = model.estimate_effect(identified_estimand,
                                        method_name="backdoor.linear_regression",
                                        control_value=(0,0),
                                        treatment_value=(1,1))
print(linear_estimate)

*** Causal Estimate ***

## Identified estimand
Estimand type: EstimandType.NONPARAMETRIC_ATE

### Estimand : 1
Estimand name: backdoor
Estimand expression:
    d
─────────(E[y|W0,W3,W2,W1])
d[v₀  v₁]
Estimand assumption 1, Unconfoundedness: If U→{v0,v1} and U→y then P(y|v0,v1,W0,W3,W2,W1,U) = P(y|v0,v1,W0,W3,W2,W1)

## Realized estimand
b: y~v0+v1+W0+W3+W2+W1+v0*X1+v0*X0+v1*X1+v1*X0
Target units: ate

## Estimate
Mean value: 19.38227351230603

More methods

You can also use methods from EconML or CausalML libraries that support multiple treatments. You can look at examples from the conditional effect notebook: https://py-why.github.io/dowhy/example_notebooks/dowhy-conditional-treatment-effects.html

Propensity-based methods do not support multiple treatments currently.