Demo for the DoWhy causal API

We show a simple example of adding a causal extension to any dataframe.

import dowhy.datasets
import dowhy.api

import numpy as np
import pandas as pd

from statsmodels.api import OLS

data = dowhy.datasets.linear_dataset(beta=5,
        num_common_causes=1,
        num_instruments = 0,
        num_samples=1000,
        treatment_is_binary=True)
df = data['df']
df['y'] = df['y'] + np.random.normal(size=len(df)) # Adding noise to data. Without noise, the variance in Y|X, Z is zero, and mcmc fails.
#data['dot_graph'] = 'digraph { v ->y;X0-> v;X0-> y;}'

treatment= data["treatment_name"][0]
outcome = data["outcome_name"][0]
common_cause = data["common_causes_names"][0]
df

	W0	v0	y
0	0.326689	False	0.448556
1	-0.906599	True	2.325172
2	0.378685	False	-1.157150
3	-0.299435	False	0.630886
4	1.042586	True	2.949594
...	...	...	...
995	0.770774	True	5.430327
996	-0.586816	True	5.585402
997	0.722458	False	1.299977
998	-0.395364	True	4.492349
999	-0.586639	True	2.965871

1000 rows × 3 columns

# data['df'] is just a regular pandas.DataFrame
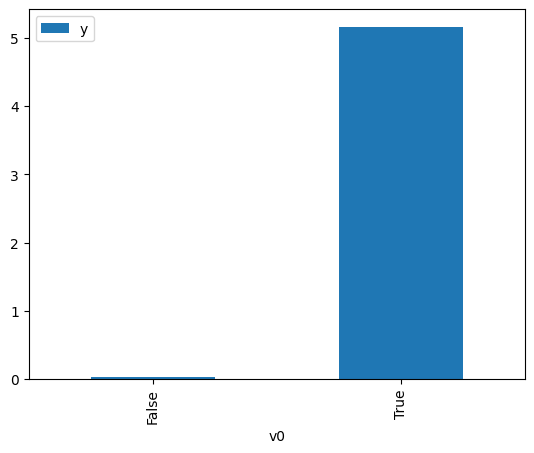
df.causal.do(x=treatment,
                     variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
                     outcome=outcome,
                     common_causes=[common_cause],
                     proceed_when_unidentifiable=True).groupby(treatment).mean().plot(y=outcome, kind='bar')

<AxesSubplot:xlabel='v0'>

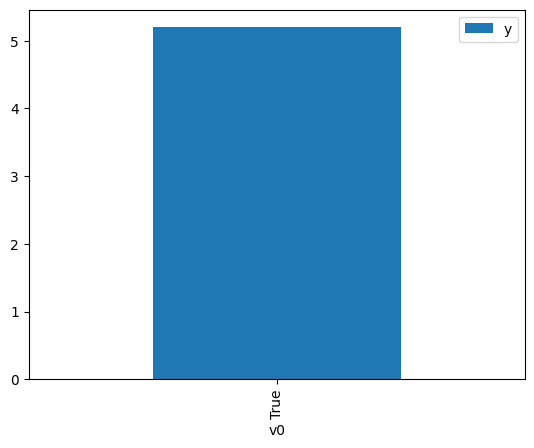
df.causal.do(x={treatment: 1},
              variable_types={treatment:'b', outcome: 'c', common_cause: 'c'},
              outcome=outcome,
              method='weighting',
              common_causes=[common_cause],
              proceed_when_unidentifiable=True).groupby(treatment).mean().plot(y=outcome, kind='bar')

<AxesSubplot:xlabel='v0'>

cdf_1 = df.causal.do(x={treatment: 1},
              variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
              outcome=outcome,
              dot_graph=data['dot_graph'],
              proceed_when_unidentifiable=True)

cdf_0 = df.causal.do(x={treatment: 0},
              variable_types={treatment: 'b', outcome: 'c', common_cause: 'c'},
              outcome=outcome,
              dot_graph=data['dot_graph'],
              proceed_when_unidentifiable=True)

cdf_0

	W0	v0	y	propensity_score	weight
0	-0.114414	False	0.806617	0.521814	1.916392
1	-0.437425	False	-1.844901	0.527280	1.896524
2	0.908197	False	1.566832	0.504479	1.982241
3	0.180203	False	-1.473251	0.516823	1.934897
4	-0.919758	False	-1.201705	0.535431	1.867655
...	...	...	...	...	...
995	-0.924271	False	-0.188714	0.535507	1.867390
996	1.820202	False	1.088118	0.489009	2.044950
997	0.039937	False	-1.274895	0.519200	1.926041
998	0.035028	False	0.371365	0.519283	1.925732
999	-1.157552	False	0.901272	0.539442	1.853767

1000 rows × 5 columns

cdf_1

	W0	v0	y	propensity_score	weight
0	2.356333	True	6.847476	0.520077	1.922793
1	1.841864	True	6.748936	0.511358	1.955578
2	-0.758494	True	4.397192	0.467292	2.139988
3	-0.741826	True	5.669855	0.467574	2.138699
4	-2.428560	True	2.266709	0.439216	2.276786
...	...	...	...	...	...
995	-1.083720	True	5.126413	0.461803	2.165426
996	-0.411489	True	3.131912	0.473158	2.113458
997	-2.217379	True	2.438822	0.442748	2.258620
998	-1.247205	True	4.836007	0.459047	2.178427
999	-0.586639	True	2.965871	0.470196	2.126771

1000 rows × 5 columns

Comparing the estimate to Linear Regression

First, estimating the effect using the causal data frame, and the 95% confidence interval.

(cdf_1['y'] - cdf_0['y']).mean()

$\displaystyle 5.08778423567129$

1.96*(cdf_1['y'] - cdf_0['y']).std() / np.sqrt(len(df))

$\displaystyle 0.102090330103608$

Comparing to the estimate from OLS.

model = OLS(np.asarray(df[outcome]), np.asarray(df[[common_cause, treatment]], dtype=np.float64))
result = model.fit()
result.summary()

OLS Regression Results

Dep. Variable:	y	R-squared (uncentered):	0.934
Model:	OLS	Adj. R-squared (uncentered):	0.934
Method:	Least Squares	F-statistic:	7076.
Date:	Wed, 14 Sep 2022	Prob (F-statistic):	0.00
Time:	18:55:14	Log-Likelihood:	-1395.1
No. Observations:	1000	AIC:	2794.
Df Residuals:	998	BIC:	2804.
Df Model:	2
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
x1	0.7558	0.031	24.243	0.000	0.695	0.817
x2	5.0264	0.045	111.891	0.000	4.938	5.115

Omnibus:	0.256	Durbin-Watson:	2.046
Prob(Omnibus):	0.880	Jarque-Bera (JB):	0.322
Skew:	0.031	Prob(JB):	0.851
Kurtosis:	2.938	Cond. No.	1.48

Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.