Confounding Example: Finding causal effects from observed data

Suppose you are given some data with treatment and outcome. Can you determine whether the treatment causes the outcome, or the correlation is purely due to another common cause?

import os, sys
sys.path.append(os.path.abspath("../../"))

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import math
import dowhy
from dowhy.do_why import CausalModel
import dowhy.datasets, dowhy.plotter

Let’s create a mystery dataset for which we need to determine whether there is a causal effect.

Creating the dataset. It is generated from either one of two models: * Model 1: Treatment does cause outcome. * Model 2: Treatment does not cause outcome. All observed correlation is due to a common cause.

rvar = 1 if np.random.uniform() >0.5 else 0
data_dict = dowhy.datasets.xy_dataset(10000, effect=rvar, sd_error=0.2)
df = data_dict['df']
print(df[["Treatment", "Outcome", "w0"]].head())

   Treatment    Outcome        w0
0   9.226765  17.942530  3.064244
1   5.627733  11.675522 -0.379016
2   9.593378  19.594728  3.692605
3   6.347941  12.917889  0.480172
4   2.806808   5.247733 -3.304526

dowhy.plotter.plot_treatment_outcome(df[data_dict["treatment_name"]], df[data_dict["outcome_name"]],
                             df[data_dict["time_val"]])

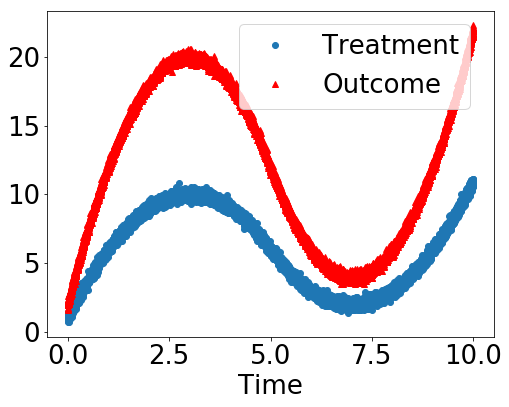
Using DoWhy to resolve the mystery: Does Treatment cause Outcome?

STEP 1: Model the problem as a causal graph

Initializing the causal model.

model= CausalModel(
        data=df,
        treatment=data_dict["treatment_name"],
        outcome=data_dict["outcome_name"],
        common_causes=data_dict["common_causes_names"],
        instruments=data_dict["instrument_names"])
model.view_model(layout="dot")

WARNING:dowhy.do_why:Causal Graph not provided. DoWhy will construct a graph based on data inputs.
INFO:dowhy.do_why:Model to find the causal effect of treatment ['Treatment'] on outcome ['Outcome']

Showing the causal model stored in the local file “causal_model.png”

from IPython.display import Image, display
display(Image(filename="causal_model.png"))

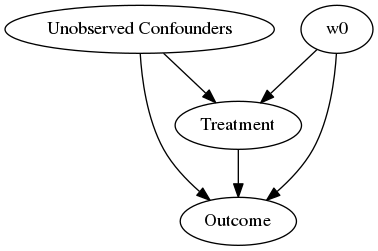
STEP 2: Identify causal effect using properties of the formal causal graph

Identify the causal effect using properties of the causal graph.

identified_estimand = model.identify_effect()
print(identified_estimand)

INFO:dowhy.causal_identifier:Common causes of treatment and outcome:['w0', 'U']
WARNING:dowhy.causal_identifier:There are unobserved common causes. Causal effect cannot be identified.

WARN: Do you want to continue by ignoring these unobserved confounders? [y/n] y

INFO:dowhy.causal_identifier:Instrumental variables for treatment and outcome:[]

Estimand type: ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
    d
──────────(Expectation(Outcome|w0))
dTreatment
Estimand assumption 1, Unconfoundedness: If U→Treatment and U→Outcome then P(Outcome|Treatment,w0,U) = P(Outcome|Treatment,w0)
### Estimand : 2
Estimand name: iv
No such variable found!

STEP 3: Estimate the causal effect

Once we have identified the estimand, we can use any statistical method to estimate the causal effect.

Let’s use Linear Regression for simplicity.

estimate = model.estimate_effect(identified_estimand,
        method_name="backdoor.linear_regression")
print("Causal Estimate is " + str(estimate.value))

# Plot Slope of line between treamtent and outcome =causal effect
dowhy.plotter.plot_causal_effect(estimate, df[data_dict["treatment_name"]], df[data_dict["outcome_name"]])

INFO:dowhy.causal_estimator:INFO: Using Linear Regression Estimator
INFO:dowhy.causal_estimator:b: Outcome~Treatment+w0

Treatment
Causal Estimate is 0.0051827863049

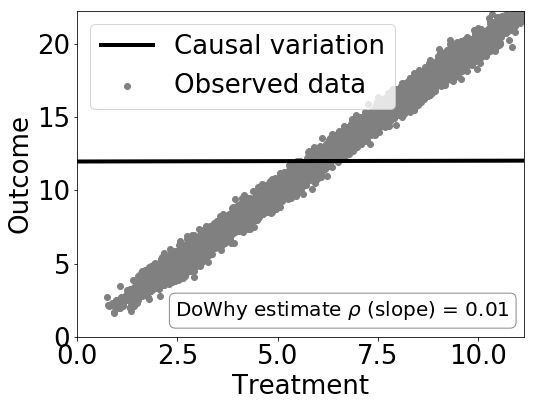
Checking if the estimate is correct

print("DoWhy estimate is " + str(estimate.value))
print ("Actual true causal effect was {0}".format(rvar))

DoWhy estimate is 0.0051827863049
Actual true causal effect was 0

Step 4: Refuting the estimate

We can also refute the estimate to check its robustness to assumptions (aka sensitivity analysis, but on steroids).

Adding a random common cause variable

res_random=model.refute_estimate(identified_estimand, estimate, method_name="random_common_cause")
print(res_random)

INFO:dowhy.causal_estimator:INFO: Using Linear Regression Estimator
INFO:dowhy.causal_estimator:b: Outcome~Treatment+w0+w_random

['Treatment']
Treatment
Refute: Add a Random Common Cause
Estimated effect:(0.0051827863049019127,)
New effect:(0.0052748828365418695,)

Replacing treatment with a random (placebo) variable

res_placebo=model.refute_estimate(identified_estimand, estimate,
        method_name="placebo_treatment_refuter", placebo_type="permute")
print(res_placebo)

INFO:dowhy.causal_estimator:INFO: Using Linear Regression Estimator
INFO:dowhy.causal_estimator:b: Outcome~placebo+w0

['Treatment']
placebo
Refute: Use a Placebo Treatment
Estimated effect:(0.0051827863049019127,)
New effect:(0.0013214086372636913,)

Removing a random subset of the data

res_subset=model.refute_estimate(identified_estimand, estimate,
        method_name="data_subset_refuter", subset_fraction=0.9)
print(res_subset)

INFO:dowhy.causal_estimator:INFO: Using Linear Regression Estimator
INFO:dowhy.causal_estimator:b: Outcome~Treatment+w0

['Treatment']
Treatment
*** Causal Estimate ***

## Target estimand
Estimand type: ate
### Estimand : 1
Estimand name: backdoor
Estimand expression:
    d
──────────(Expectation(Outcome|w0))
dTreatment
Estimand assumption 1, Unconfoundedness: If U→Treatment and U→Outcome then P(Outcome|Treatment,w0,U) = P(Outcome|Treatment,w0)
### Estimand : 2
Estimand name: iv
No such variable found!

## Realized estimand
b: Outcome~Treatment+w0
## Estimate
Value: 0.0032596514859678217

Refute: Use a subset of data
Estimated effect:(0.0051827863049019127,)
New effect:(0.0032596514859678217,)

As you can see, our causal estimator is robust to simple refutations.